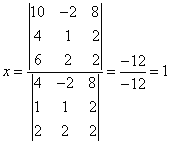Parámetro que define un sistema ecuaciones como determinado o no

Dado el sistema, 

 

a) Para qué valores del parámetro el sistema es compatible determinado?

 Para ser un sistema compatible determinado el rango de la matriz de coeficientes tiene que coincidir con el rango de la matriz ampliada y coincidir con el número de incógnitas. Cómo que tenemos 3 incógnitas y tres ecuaciones, sólo hay que encontrar los valores del parámetro para los cuales el determinante de la matriz de coeficientes del sistema sea diferente de cero.

Calculamos el rango de la matriz de coeficientes haciendo su determinante,

Si  a al cuadrado - 16 = 0, entonces a = 4 y a = - 4 . Por lo tanto, el sistema es compatible determinado cuándo a es diferente a 4 y -4 . En cambio,  el determinante de la matriz es cero y el rango de la matriz de coeficientes es inferior a 3.

b) ¿Para qué valores del parámetro el sistema es incompatible? 

El sistema no es compatible determinado para a = 4 y a = - 4
 

 Veremos que pasa para a = 4

 

La matriz de coeficientes del sistema es, 

y la matriz ampliada es 

Buscamos una matriz de orden 3 con determinante diferente de cero, 

Así el rango de la matriz ampliada es 3, diferente del rango de la matriz de coeficientes. Por lo tanto, el sistema es incompatible para a = 4

Si analizamos que sucede para a = - 4, entonces
La matriz de coeficientes del sistema es, 

y la matriz ampliada es 

Buscamos una matriz de orden 3 con determinante diferente de cero, 

Por lo tanto, el rango de la matriz ampliada es 3, y por los razonamientos anteriores, el sistema también es incompatible para a = - 4.




c) ¿ Para qué valores del parámetro el sistema es compatible indeterminado? 

c) Para ningún valor del parámetro el sistema es compatible indeterminado, como se deduce de los apartados anteriores.  

 
d) Resolvéis el sistema para a = 2:

Y por Gauss,

Hemos llegado a:

Por tanto x = y = z = 1

Por Cramer:

Plantear un sistema de ecuaciones

Una empresa fabrica tres artículos, A, B y C, que vende en tres mercados diferentes a los que denominaremos “Mercado Norte”, “Mercado Sur” y “Mercado Centro”. Las unidades vendidas en un día de cada artículo a cada uno de los mercados, vienen dadas por la tabla siguiente:

	Precio	Unidades vendidas mercado norte	Unidades vendidas mercado sur	Unidades vendidas mercado centro
Articulo A	x	4	0	6
Articulo B	y	3	4	2
Articulo C	z	2	1	0

Se pide:

a) Plantear el sistema de ecuaciones que determina el precio de venta de cada uno de los artículos (x,y,z), si sabemos que los ingresos por ventas diarias al Mercado Norte, Mercado Sur y Mercado Centro son 14€, 10€ y 10€ respectivamente.
a) Resolver el sistema de ecuaciones planteado en el apartado anterior.
b) Si el coste de producción unitario del artículo A es 0.5€, el coste del artículo B es de 1€, y el coste del artículo C asciende a 0.75€, cuál es el beneficio que obtiene la empresa en un día?  

Nota: Beneficios = Ingresos – Costes.

a)      El sistema de ecuaciones es:

4x + 3y + 2z = 14
4y + z = 10
6x + 2y = 10

b) Comprobamos si el sistema es compatible determinado haciendo el determinante de la matriz de coeficientes,

Como que es diferente de cero, el rango de la matriz y el de la matriz ampliada coinciden y, además, coinciden con el número de incógnitas. Por lo tanto, es compatible determinado y, dado que el determinante es diferente de cero, podemos aplicar Cramer para encontrar la solución. Así,

Por lo tanto, los precios de los artículos A,B y C son respectivamente de 1uno.m., 2 uno.m. y 2 uno.m.
Si resolvemos por Gauss, al primer paso multiplicando la primera fila por (-6/4) y sumando la tercera, y después multiplicando la segunda fila por (5/8) y sumando la tercera, obtenemos,

 Así tenemos,

Y, por lo tanto, obtenemos x = 1 , y = 2 y z = 2.

c)

Beneficio artículo A = (precio venta unitario - coste unitario) • número de artículos A = (1 - 0.5)•10 = 5

Beneficio artículo B = (precio venta unitario - coste unitario) • número de artículos B = (2 - 1)•9 = 9

Beneficio artículo C = (precio venta unitario - coste unitario) • número de artículos C = (2 - 0.75)•3 = 3.75 

Por lo tanto, el beneficio total es de 5 + 9 + 3.75 = 17.75 un.m.

 

Sistema de ecuaciones compatible indeterminado

En esta entrada vamos a exponer el siguiente ejemplo, ¿Cuánto tiene que valer para que el sistema de ecuaciones sea compatible indeterminado?

Es un sistema homogéneo, por lo tanto seguro que tiene al menos una solución, . Por lo tanto, el sistema es compatible y por el teorema de Rouche, entonces, el rango de la matriz de los coeficientes es igual al rango de la matriz ampliada. Para ser compatible indeterminado hará falta que el rango de las matrices sea inferior a 2.


a) Por Gauss, multiplicando la primera fila por (-1/5) y sumando la segunda,

 

 

Si 2 + a = 0, es decir si , a= - 2 el rango de la matriz es 1, y como el número de incógnitas es 2, el sistema es compatible indeterminado.
Si a es diferente de 2 , el rango de la matriz es 2, y cómo coincide con el número de incógnitas, el sistema es compatible determinado.




b) Por determinantes,

 

Igualamos a 0. Si el determinante es nulo, el rango de la matriz es igual a 1. Por lo tanto,

10 + 5a = 0 ; a = - 2

Así para el sistema es compatible indeterminado.